Print bookPrint book

LESSON: Congruent and Similar Figures

Congruent and Similar Figures

Site: Mountain Heights Academy OpenCourseWare
Course: Mathematics Essentials Q4 v2013
Book: LESSON: Congruent and Similar Figures
Printed by: Guest user
Date: Sunday, 22 October 2017, 9:56 AM

Table of contents

Objectives/Vocab

Objectives

  • Identify given triangles as similar, congruent or neither.
  • Identify corresponding parts of congruent figures.
  • Identify corresponding parts of similar figures.
  • Find unknown measures of corresponding parts of similar figures.
  • Use similar figures to measure indirectly.

Vocabulary

Congruent
having the same size and shape and measurement
Similar
having the same shape, but not the same size. Similar shapes are proportional to each other.
Corresponding
matching-corresponding sides between two triangles are sides that match up
Ratio
a way of comparing two quantities
Proportion
a pair of equal ratios.
Indirect Measurement
using the characteristics of similar triangles to measure challenging things or distances.
     

WATCH: Similar Figures

WATCH: Similar vs Congruent

READ: Identify Given Triangles as Similar, Congruent or Neither

Identify Given Triangles as Similar, Congruent or Neither

You have heard the word congruent used regarding line segments being the same length. The word congruent can apply to other things in geometry besides lines and line segments. Congruent means being exactly the same. When two line segments have the same length, we can say that they are congruent. When two figures have the same shape, we can say that the two figures are congruent.


Example

These two triangles are congruent. They are exactly the same in every way. They are the same size and the same shape. We can also say that their side lengths are the same and that their angle measures are the same.


Sometimes, two figures will be similar. Similar means that the figures have the same shape, but not the same size. Similar figures are not congruent.


Example

These two triangles are similar. They are the same shape, but they are not the same size.


Example

These two triangles are neither congruent or similar.

READ: Identify Corresponding Parts of Congruent Figures

Identify Corresponding Parts of Congruent Figures

Now that you understand the difference between congruent figures and similar figures, we can look at the corresponding parts of congruent triangles. The word corresponding refers to parts that match between two congruent triangles. We can identify corresponding angles and corresponding sides.


Example

First, we can name the corresponding angles. Corresponding angles are matching angles between the two triangles. Corresponding angles will have the same measure in congruent triangles.

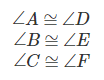
\angle{A} \cong \angle{D} \\ \angle{B} \cong \angle{E} \\ \angle{C} \cong \angle{F}

Here the angles are connected with the symbol for congruent. When you see the equals sign with a squiggly line on top, you know that we are looking at the symbol for congruent.

Next, we can name the corresponding sides. Corresponding sides are matching sides between two triangles. They will have the same length in congruent triangles.

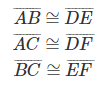
\overline{AB} \cong \overline{DE} \\ \overline{AC} \cong \overline{DF} \\ \overline{BC} \cong \overline{EF}

EXAMPLE 4

READ: Identify Corresponding Parts of Similar Figures

Identify Corresponding Parts of Similar Figures

We just finished identifying the corresponding parts of congruent figures, and we can also identify the corresponding parts of similar figures. We do this in the same way. Let’s look at an example.


Example

Triangle ABC is similar to triangle DEF. This means that while they are the same shape, they aren’t the same size. In fact, there is a relationship between the corresponding parts of the triangle.

The side lengths are corresponding even though they aren’t congruent.

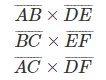
\overline{AB} \times \overline{DE} \\ \overline{BC} \times \overline{EF} \\ \overline{AC} \times \overline{DF}

We used the symbol for similar to show the relationship between the corresponding sides of the two triangles.

WATCH: Investigating Congruent Triangles

READ: Find Unknown Measures of Corresponding Parts of Similar Figures

Find Unknown Measures of Corresponding Parts of Similar Figures

There is also a relationship between the sides of similar triangles. Once you know how to locate the corresponding sides of similar triangles, we can write ratios to compare the lengths of sides. Let’s look at an example.


Example

First, we can identify the corresponding sides of these two similar triangles.

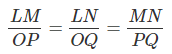
\frac{LM}{OP} = \frac{LN}{OQ} = \frac{MN}{PQ}

Now we have been given side lengths for each pair of corresponding sides. These have been written in a proportion or a set of three equal ratios. Remember that there is a relationship between the corresponding sides because they are parts of similar triangles. The side lengths of the similar triangles form a proportion.

Let’s substitute the given formula into our proportion.

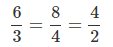
\frac{6}{3} = \frac{8}{4} = \frac{4}{2}

There is a pattern with the ratios of corresponding sides. You can see that the measurement of the each side of the first triangle divided by two is the measure of the corresponding side of the second triangle.


We can use patterns like this to problem solve the length of missing sides of similar triangles.


Example

Here we have two similar triangles. One is larger than the other, but they are similar. They have the same shape but a different size. Therefore, the corresponding sides are similar.

If you look at the side lengths, there is one variable. That is the missing side length. We can figure out the missing side length by using proportions. We know that the corresponding side lengths form a proportion. Let’s write ratios that form a proportion and find the pattern to figure out the length of the missing side.

\frac{AB}{DE} & = \frac{AC}{DF} = \frac{BC}{EF} \\ \frac{5}{10} & = \frac{15}{x} = \frac{10}{20}

Looking at this you can see the pattern. The side lengths of the second triangle are double the length of the corresponding side of the first triangle.

Using this pattern, you can see that the length of DF in the second triangle will be twice the length of AC. The length of AC is 15.

15 * 2 = 30

The length of DF is 30.

EXAMPLE 5

READ: Use Similar Figures to Measure Indirectly

Use Similar Figures to Measure Indirectly

We can use the properties of similar figures to measure things that are challenging to measure. We call this type of measurement indirect measurement.

Let’s look at an example so that we can understand indirect measurement.


Jamie’s Dad is six feet tall. Standing outside, his shadow is eight feet long. A tree is next to him. The tree has a shadow that is sixteen feet long. Given these dimensions, how tall is the tree?

If you think about a tree, it makes a shadow and the line from the end of the shadow to the top of the tree creates a triangle. It sounds confusing, but here is a diagram to help you.

Here is a palm tree. You can see from the picture that the tree itself is one side of the triangle, that the shadow length is another side of the triangle and that the diagonal from the top of the tree to the top of the shadow forms the hypotenuse of the triangle.

How would this work with the shadow of a person? Let’s look at an example.

There is a triangle here too. Just because it is on an angle don’t let that fool you. It is still a triangle.


Jamie’s Dad is six feet tall. Standing outside, his shadow is eight feet long. A tree is next to him. The tree has a shadow that is sixteen feet long. Given these dimensions, how tall is the tree?

To solve this, we have to create two ratios. One will compare the heights of the man and the tree the other will compare the lengths of the shadows. Together, they will form a proportion because similar triangles are proportional and we have already seen how triangles are created with people or things and shadows.

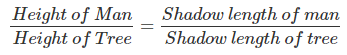
\frac{Height\ of\ Man}{Height\ of\ Tree} = \frac{Shadow\ length\ of\ man}{Shadow\ length\ of\ tree}

Notice that we compare the same things in each ratio. The first compares heights, the second compares shadow length. This is key when working with similar triangles and indirect measurement. Be sure to compare like things! Now we can fill in the given information.

\frac{6’}{x} = \frac{8’}{16’}

We are looking for the height of the tree, so that is where our variable goes. Now we can solve the proportion.

Our answer is 12 feet. The tree is 12 feet tall.

You can use similar triangles and proportions to measure difficult things. Indirect measurement makes the impossible seem possible!!

CHECK Yourself! Finding Measures of Similar Figures